Gezhikaiwu(讨论 | 贡献) (添加无向图) |
Gezhikaiwu(讨论 | 贡献) 无编辑摘要 |
||
| (未显示同一用户的1个中间版本) | |||
| 第2行: | 第2行: | ||
==概念== | ==概念== | ||
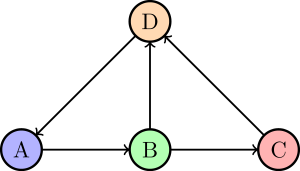
[[File:有向图.png|alt=有向图|thumb|有向图]] | |||
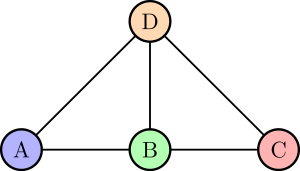
[[File:无向图HD.png|alt=无向图|thumb|无向图]] | |||
'''图的定义''':图<math>G=(V, E)</math>是由顶点集<math>V</math>和边集<math>E</math>组成的,其中<math>V</math>是非空有限集合,<math>E</math>是<math>V</math>中元素对(无向图)或有序对(有向图)所组成的集合。 | '''图的定义''':图<math>G=(V, E)</math>是由顶点集<math>V</math>和边集<math>E</math>组成的,其中<math>V</math>是非空有限集合,<math>E</math>是<math>V</math>中元素对(无向图)或有序对(有向图)所组成的集合。 | ||
| 第17行: | 第19行: | ||
# 悬点(Pendant Vertex):恰有一条关联边的顶点称为悬点。 | # 悬点(Pendant Vertex):恰有一条关联边的顶点称为悬点。 | ||
# 悬边(Pendant Edge):与悬点关联的边称为悬边。 | # 悬边(Pendant Edge):与悬点关联的边称为悬边。 | ||
==历史== | ==历史== | ||
图论的历史始于1736年,欧拉通过解决柯尼斯堡七桥问题,奠定了图论的基础。在19世纪和20世纪,随着数学家们对图论问题的研究,图论逐渐发展为一个成熟的数学领域。20世纪下半叶,随着计算机科学的发展,图论在计算机科学中的应用越来越广泛,成为计算机科学的一个重要分支。 | 图论的历史始于1736年,欧拉通过解决柯尼斯堡七桥问题,奠定了图论的基础。在19世纪和20世纪,随着数学家们对图论问题的研究,图论逐渐发展为一个成熟的数学领域。20世纪下半叶,随着计算机科学的发展,图论在计算机科学中的应用越来越广泛,成为计算机科学的一个重要分支。 | ||
2023年4月28日 (五) 18:24的最新版本
图论是数学的一个分支,研究图的数学性质。图论中的图由顶点(或节点)和连接它们的边(或弧)组成。图论的概念可追溯到1736年,欧拉用图论解决了柯尼斯堡七桥问题。此后,图论逐渐发展为一个成熟的数学领域,并在计算机科学、网络科学、生物学等多个领域得到了广泛应用。
概念
图的定义:图是由顶点集和边集组成的,其中是非空有限集合,是中元素对(无向图)或有序对(有向图)所组成的集合。
- 边(Edge):边是图中连接两个顶点的线段。在无向图中,边是顶点对,顺序无关;在有向图中,边是顶点的有序对,顺序相关,表示从顶点指向顶点。
- 端点(Endpoint):边连接的两个顶点称为端点。设边,则顶点和是边的端点。
- 环(Loop):如果一条边的两个端点重合,即,则称为环。
- 空图(Empty Graph):一个没有顶点和边的图称为空图。
- 零图(Null Graph):一个有个顶点但没有边的图称为图,也叫零图。
- 平凡图(Trivial Graph):只有一个顶点的图称为平凡图,记为图。
- 简单图(Simple Graph):没有环和平行边(具有相同端点的多条边)的图称为简单图。
- 偶图(Bipartite Graph):如果图的顶点集能分解为两个不相交子集和(即,),且子集内的顶点互不相邻,则称图是偶图,记为。
- 有向图(Directed Graph):图称为有向图,如果边集由顶点集中元素的有序对组成。在有向图中,顶点是边的尾,边与顶点出关联;顶点是边的头,边与顶点入关联。
- 无向图(Undirected Graph):图称为无向图,如果边集由顶点集中元素的无序对组成。
- 孤立点(Isolated Vertex):没有关联边的顶点称为孤立点。
- 悬点(Pendant Vertex):恰有一条关联边的顶点称为悬点。
- 悬边(Pendant Edge):与悬点关联的边称为悬边。
历史
图论的历史始于1736年,欧拉通过解决柯尼斯堡七桥问题,奠定了图论的基础。在19世纪和20世纪,随着数学家们对图论问题的研究,图论逐渐发展为一个成熟的数学领域。20世纪下半叶,随着计算机科学的发展,图论在计算机科学中的应用越来越广泛,成为计算机科学的一个重要分支。
图论问题
- 图的计数:计算某类图的数量。例如,计算具有个顶点的无向图的数量。
- 子图相关问题:在给定的图中寻找具有特定性质的子图。例如:
- 子图同构问题:给定两个图和,判断中是否存在一个子图与同构。这是一个NP完全问题。
- 哈密顿回路问题:给定一个图,判断是否存在一个子图与具有个顶点的圈同构。
- 染色问题:将图的顶点或边染色,使得满足特定条件。例如:
- 四色问题:证明任何平面图的顶点可以用不超过四种颜色染色,使得相邻顶点具有不同颜色。
- 边色数问题:求一个图的最少边色数,使得相邻边具有不同颜色。
- 路径问题:在给定的图中寻找满足特定条件的路径。例如:
- 柯尼斯堡七桥问题:求解是否存在一条经过柯尼斯堡七桥且仅经过一次的路径。
- 哈密顿回路问题:在给定图中寻找一条包含所有顶点且仅访问一次的回路。
- 最小生成树问题:在给定的带权无向图中寻找权值最小的生成树。
- 中国邮路问题:求解经过所有边至少一次的最短路径。
- 最短路问题:求解给定两个顶点之间的最短路径。
- 斯坦纳树:求解包含给定顶点集合的最小生成树。
- 旅行商问题:求解经过所有顶点且仅访问一次的最短路径(NP困难问题)。
- 网络流与匹配问题:
- 最大流问题、最小割问题和最大流最小割定理:在给定的网络中求解最大流和最小割。
- 最小费用最大流问题:在给定的网络中求解具有最小费用的最大流。
- 二分图及任意图上的最大匹配:求解给定图中的最大匹配。
- 带权二分图的最大权匹配:求解给定带权二分图中的最大权匹配。
- 覆盖问题:
- 最大团:在给定图中寻找最大的完全子图。
- 最大独立集:在给定图中寻找最大的无边导出子图,即独立集。
- 最小覆盖集:求解包含所有顶点的最小边集。
- 最小支配集:求解能支配给定图中所有顶点的最小顶点集。
重要算法
- 迪克斯特拉算法(Dijkstra's Algorithm, D.A):求解给定图中两个顶点之间的最短路径。
- 克鲁斯卡尔算法(Kruskal's Algorithm, K.A):求解给定带权无向图的最小生成树。
- 普里姆算法(Prim's Algorithm, P.A):求解给定带权无向图的最小生成树。
- 拓扑排序算法(Topological Sorting Algorithm, TSA):对有向无环图(DAG)进行拓扑排序。
- 关键路径算法(Critical Path Algorithm, CPA):求解给定图中的关键路径。
- 广度优先搜索算法(Breadth-First Search, BFS):对图进行广度优先遍历。
- 深度优先搜索算法(Depth-First Search, DFS):对图进行深度优先遍历。