海伦公式

海倫公式 (Heron's formula)

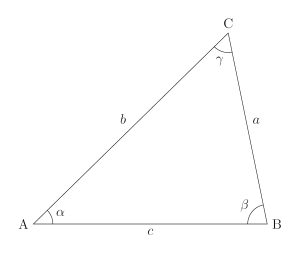
海倫公式，以古希臘數學家海倫（Heron of Alexandria）的名字命名，是用於計算任意三角形面積的公式。該公式適用於已知三角形三邊長度的情況。

定義

設三角形的三邊長分別為 $a$、$b$ 和 $c$，其半周長記為 $s$，則海倫公式可以表示為：

$s={\frac {a+b+c}{2}}$

三角形的面積 $A$ 可以通過以下公式計算：

$A={\sqrt {s(s-a)(s-b)(s-c)}}$

歷史背景

海倫公式起源於古希臘，由海倫（公元10 - 70年）提出。海倫是一位著名的數學家和工程師，他的工作主要集中在幾何、物理和工程學等領域。海倫公式是他在《度量論》（Metrica）一書中提出的，這本書是關於幾何測量的綜合性著作。

推導

海倫公式的推導可以分為以下幾個步驟：

1. 首先，定義半周長 $s$ 為三邊之和的一半，即 $s={\frac {a+b+c}{2}}$。

2. 考慮到任意一個角，例如角 $\gamma$，我們可以用餘弦定理表示為：

  $\cos \gamma ={\frac {a^{2}+b^{2}-c^{2}}{2ab}}$

3. 然後，利用正弦定理，我們可以知道 $\sin \gamma ={\sqrt {1-\cos ^{2}\gamma }}$。

4. 三角形的面積可以表示為 $A={\frac {1}{2}}ab\sin \gamma$。

5. 通過將餘弦定理和正弦定理結合，並替換為半周長的形式，可以得到：

  $A={\frac {1}{2}}ab{\sqrt {1-\left({\frac {a^{2}+b^{2}-c^{2}}{2ab}}\right)^{2}}}$

6. 經過數學上的變形和簡化，最終可以得到海倫公式的標準形式：

  $A={\sqrt {s(s-a)(s-b)(s-c)}}$

應用

海倫公式在各個領域都有廣泛的應用，尤其是在土木工程、建築設計、航空航天和計算機圖形學等領域。它為計算不規則形狀的面積提供了一種有效的數學工具，特別是在只知道邊長而不知道角度的情況下。

總的來說，海倫公式是數學領域中一個重要的公式，它不僅具有重要的理論價值，同時也在實際應用中發揮着重要作用。