Gezhikaiwu(讨论 | 贡献) (→推导) |
Gezhikaiwu(讨论 | 贡献) (→推导) |
||
| 第32行: | 第32行: | ||
<math> | <math> | ||
BD^2 = c^2 - AD^2 | |||
</math> | |||
3. 同理,在直角三角形 CBD 中: | 3. 同理,在直角三角形 CBD 中: | ||
<math> | <math> | ||
BD^2 = a^2 - CD^2 | |||
</math> | </math> | ||
4. 注意到 | 4. 注意到 AD 可以表示为: | ||
<math> | <math> | ||
AD = b - CD | |||
</math> | </math> | ||
5. 将 CD 的表达式代入步骤 | 5. 将 CD 的表达式代入步骤 2 中的等式,得到: | ||
<math> | <math> | ||
BD^2=c^2-(b-CD)^2 | |||
</math> | </math> | ||
| 第56行: | 第56行: | ||
<math> | <math> | ||
a^2 - CD^2=c^2-b^2-CD^2+2b\cdot CD | |||
</math> | |||
即: | |||
<math> | |||
a^2+b^2-c^2=2b\cdot CD | |||
</math> | </math> | ||
7. 现在,我们利用余弦的定义。在三角形 ABC 中,角 | 7. 现在,我们利用余弦的定义。在三角形 ABC 中,角<math> \gamma </math> 的余弦是: | ||
<math> | <math> | ||
\cos \gamma = \frac{ | \cos \gamma = \frac{CD}{a} | ||
</math> | </math> | ||
8. 将 | 8. 将 CD 用 a 和 cos \gamma 表示,即: | ||
<math> | <math> | ||
CD = a \cdot \cos \gamma | |||
</math> | </math> | ||
| 第74行: | 第78行: | ||
<math> | <math> | ||
c^2 = a^2 + b^2 - 2ab \cdot \cos \gamma | c^2=a^2+b^2-2ab\cdot \cos \gamma | ||
</math> | </math> | ||
2023年11月11日 (六) 02:37的最新版本
余弦定理(Cosine Theorem)
余弦定理是一个在几何中非常重要的定理,主要用于计算任意三角形的边长和角度。它是勾股定理的一种推广形式,适用于所有类型的三角形,包括钝角三角形和锐角三角形。
定义
余弦定理表明,在任意三角形中,一个角的余弦值可以通过其他两边的长度和夹角所对的边的长度来计算。具体来说,如果一个三角形的边长分别是 、 和 ,且这些边对应的对角分别是 、 和 ,那么余弦定理可以表示为:
同理,
历史背景
余弦定理的历史可以追溯到古代数学,最初由希腊数学家在研究三角形时提出。这一定理在不同的文化中有着不同的发展历程,包括在印度、伊斯兰和欧洲的数学传统中。
推导
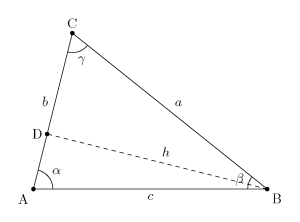
考虑一个任意三角形 ABC。我们的目标是推导出余弦定理的公式。余弦定理的一个常见形式是:
1. 从点 B 向 AC 边作垂线,假设垂足为 D。这样,三角形 ABC 被分成了两个直角三角形 ABD 和 CBD。
2. 在直角三角形 ABD 中,根据勾股定理,我们有:
3. 同理,在直角三角形 CBD 中:
4. 注意到 AD 可以表示为:
5. 将 CD 的表达式代入步骤 2 中的等式,得到:
6. 展开并简化上式,我们可以得到:
即:
7. 现在,我们利用余弦的定义。在三角形 ABC 中,角的余弦是:
8. 将 CD 用 a 和 cos \gamma 表示,即:
9. 将此表达式代入步骤 6 中的等式,我们得到余弦定理的最终形式:
这样,我们就完成了余弦定理的推导。
应用
余弦定理在多个领域中都有广泛应用,包括物理、工程学、天文学以及航海学。它不仅用于解决几何问题,还在解析力学和信号处理等领域中发挥着重要作用。
在实际应用中,余弦定理常用于确定未知边长或角度,特别是在无法直接测量的情况下。例如,它可以用于地图制作、航海定位和建筑设计中的测量计算。