余弦定理

餘弦定理（Cosine Theorem）

餘弦定理是一個在幾何中非常重要的定理，主要用於計算任意三角形的邊長和角度。它是勾股定理的一種推廣形式，適用於所有類型的三角形，包括鈍角三角形和銳角三角形。

定義

餘弦定理表明，在任意三角形中，一個角的餘弦值可以通過其他兩邊的長度和夾角所對的邊的長度來計算。具體來說，如果一個三角形的邊長分別是 $a$、$b$ 和 $c$，且這些邊對應的對角分別是 $\alpha$、$\beta$ 和 $\gamma$，那麼餘弦定理可以表示為：

$c^{2}=a^{2}+b^{2}-2ab\cdot \cos \gamma$

同理，

$a^{2}=b^{2}+c^{2}-2bc\cdot \cos \alpha$

$b^{2}=a^{2}+c^{2}-2ac\cdot \cos \beta$

歷史背景

餘弦定理的歷史可以追溯到古代數學，最初由希臘數學家在研究三角形時提出。這一定理在不同的文化中有着不同的發展歷程，包括在印度、伊斯蘭和歐洲的數學傳統中。

推導

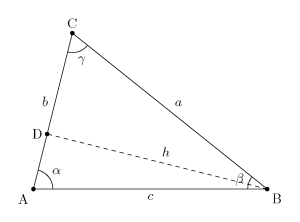
考慮一個任意三角形 ABC。我們的目標是推導出餘弦定理的公式。餘弦定理的一個常見形式是：

$c^{2}=a^{2}+b^{2}-2ab\cdot \cos \gamma$

1. 從點 B 向 AC 邊作垂線，假設垂足為 D。這樣，三角形 ABC 被分成了兩個直角三角形 ABD 和 CBD。

2. 在直角三角形 ABD 中，根據勾股定理，我們有：

  $BD^{2}=c^{2}-AD^{2}$

3. 同理，在直角三角形 CBD 中：

  $BD^{2}=a^{2}-CD^{2}$

4. 注意到 AD 可以表示為：

  $AD=b-CD$

5. 將 CD 的表達式代入步驟 2 中的等式，得到：

  $BD^{2}=c^{2}-(b-CD)^{2}$

6. 展開並簡化上式，我們可以得到：

  $a^{2}-CD^{2}=c^{2}-b^{2}-CD^{2}+2b\cdot CD$
  即：
  $a^{2}+b^{2}-c^{2}=2b\cdot CD$

7. 現在，我們利用餘弦的定義。在三角形 ABC 中，角$\gamma$的餘弦是：

  $\cos \gamma ={\frac {CD}{a}}$

8. 將 CD 用 a 和 cos \gamma 表示，即：

  $CD=a\cdot \cos \gamma$

9. 將此表達式代入步驟 6 中的等式，我們得到餘弦定理的最終形式：

  $c^{2}=a^{2}+b^{2}-2ab\cdot \cos \gamma$

這樣，我們就完成了餘弦定理的推導。

應用

餘弦定理在多個領域中都有廣泛應用，包括物理、工程學、天文學以及航海學。它不僅用於解決幾何問題，還在解析力學和信號處理等領域中發揮着重要作用。

在實際應用中，餘弦定理常用於確定未知邊長或角度，特別是在無法直接測量的情況下。例如，它可以用於地圖製作、航海定位和建築設計中的測量計算。