Gezhikaiwu(讨论 | 贡献) (→算法描述) |
Gezhikaiwu(讨论 | 贡献) (→算法描述) |
||
| 第7行: | 第7行: | ||
== 算法描述 == | == 算法描述 == | ||
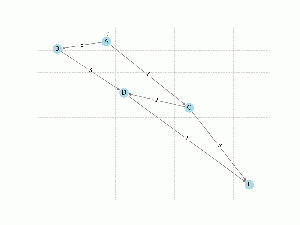
[[File:Dijkstra steps.gif|thumb]] | |||
算法的步骤如下: | 算法的步骤如下:<syntaxhighlight lang="markdown"> | ||
1. 将所有节点的最短路径估计值初始化为无穷大,将源点的最短路径估计值设为0。 | 1. 将所有节点的最短路径估计值初始化为无穷大,将源点的最短路径估计值设为0。 | ||
| 第25行: | 第24行: | ||
== 数学表示 == | == 数学表示 == | ||
设<math>G = (V, E)</math>是一个带权图,其中<math>V</math>是节点集合,<math>E</math>是边集合。对于每条边<math>(u, v) \in E</math>,其权重由函数<math>w: E \rightarrow \mathbb{R}</math>给出。Dijkstra算法可以用以下伪代码表示: | 设<math>G = (V, E)</math>是一个带权图,其中<math>V</math>是节点集合,<math>E</math>是边集合。对于每条边<math>(u, v) \in E</math>,其权重由函数<math>w: E \rightarrow \mathbb{R}</math>给出。Dijkstra算法可以用以下伪代码表示:<syntaxhighlight lang="matlab" line> | ||
function Dijkstra(Graph, source): | function Dijkstra(Graph, source): | ||
dist[source] ← 0 // 初始化源点到自身的距离为0 | dist[source] ← 0 // 初始化源点到自身的距离为0 | ||
2023年11月10日 (五) 12:15的最新版本
Dijkstra算法(Dijkstra's Algorithm)
Dijkstra算法是计算图中最短路径的算法之一,由荷兰计算机科学家艾兹赫尔·戴克斯特拉(Edsger W. Dijkstra)在1956年提出,并于1959年发表。这个算法可以找到一个节点到图中其他所有节点的最短路径,特别适用于不包含负权边的有向图和无向图。
定义
Dijkstra算法的目的是从图中的单个源点出发,计算到达所有其他节点的最短路径。其基本思想是创建一个集合,该集合跟踪已知的最短路径长度的节点。
算法描述
算法的步骤如下:
1. 将所有节点的最短路径估计值初始化为无穷大,将源点的最短路径估计值设为0。
2. 将所有节点放入未处理的集合中。
3. 当未处理的集合非空时,重复以下步骤:
a. 从未处理集合中选择一个最短路径估计值最小的节点u。
b. 将节点u标记为已处理,表示u的最短路径估计值是最终的。
c. 放松节点u的所有未处理的邻接点v。即,对于每个邻接点v,如果通过u到v的路径比当前已知的最短路径估计值短,就更新v的最短路径估计值。
数学表示
设是一个带权图,其中是节点集合,是边集合。对于每条边,其权重由函数给出。Dijkstra算法可以用以下伪代码表示:
function Dijkstra(Graph, source):
dist[source] ← 0 // 初始化源点到自身的距离为0
for each vertex v in Graph:
if v ≠ source
dist[v] ← infinity // 将其他所有节点的距离初始化为无穷大
prev[v] ← undefined // 节点的前驱节点初始化为未定义
end if
end for
Q ← the set of all nodes in Graph // 创建一个包含图中所有节点的集合Q
while Q is not empty: // 当集合Q非空时
u ← node in Q with min dist[u] // 从Q中取出距离最小的节点u
remove u from Q // 从Q中移除节点u
for each neighbor v of u: // 检查u的所有邻居v
alt ← dist[u] + length(u, v) // 计算通过u到v的距离
if alt < dist[v]: // 如果新计算的距离更短
dist[v] ← alt // 更新v的距离
prev[v] ← u // 将v的前驱节点设置为u
end if
end for
end while
return dist[], prev[]
end function
应用
Dijkstra算法在多种场景中都有应用,包括计算机网络中的路由选择、地图软件中的导航系统、社交网络中查找人际关系的最短路径等。这个算法的效率和准确性使它成为实际应用中计算最短路径的首选算法之一。
注意事项
Dijkstra算法不能处理图中存在负权边的情况,因为这可能会导致算法无法找到真正的最短路径。在包含负权边的图中,通常使用Bellman-Ford算法来计算最短路径。