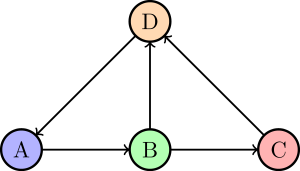
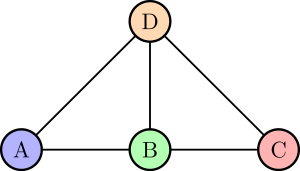
圖論是數學的一個分支,研究圖的數學性質。圖論中的圖由頂點(或節點)和連接它們的邊(或弧)組成。圖論的概念可追溯到1736年,歐拉用圖論解決了柯尼斯堡七橋問題。此後,圖論逐漸發展為一個成熟的數學領域,並在計算機科學、網絡科學、生物學等多個領域得到了廣泛應用。
概念
圖的定義:圖是由頂點集和邊集組成的,其中是非空有限集合,是中元素對(無向圖)或有序對(有向圖)所組成的集合。
- 邊(Edge):邊是圖中連接兩個頂點的線段。在無向圖中,邊是頂點對,順序無關;在有向圖中,邊是頂點的有序對,順序相關,表示從頂點指向頂點。
- 端點(Endpoint):邊連接的兩個頂點稱為端點。設邊,則頂點和是邊的端點。
- 環(Loop):如果一條邊的兩個端點重合,即,則稱為環。
- 空圖(Empty Graph):一個沒有頂點和邊的圖稱為空圖。
- 零圖(Null Graph):一個有個頂點但沒有邊的圖稱為圖,也叫零圖。
- 平凡圖(Trivial Graph):只有一個頂點的圖稱為平凡圖,記為圖。
- 簡單圖(Simple Graph):沒有環和平行邊(具有相同端點的多條邊)的圖稱為簡單圖。
- 偶圖(Bipartite Graph):如果圖的頂點集能分解為兩個不相交子集和(即,),且子集內的頂點互不相鄰,則稱圖是偶圖,記為。
- 有向圖(Directed Graph):圖稱為有向圖,如果邊集由頂點集中元素的有序對組成。在有向圖中,頂點是邊的尾,邊與頂點出關聯;頂點是邊的頭,邊與頂點入關聯。
- 無向圖(Undirected Graph):圖稱為無向圖,如果邊集由頂點集中元素的無序對組成。
- 孤立點(Isolated Vertex):沒有關聯邊的頂點稱為孤立點。
- 懸點(Pendant Vertex):恰有一條關聯邊的頂點稱為懸點。
- 懸邊(Pendant Edge):與懸點關聯的邊稱為懸邊。
歷史
圖論的歷史始於1736年,歐拉通過解決柯尼斯堡七橋問題,奠定了圖論的基礎。在19世紀和20世紀,隨著數學家們對圖論問題的研究,圖論逐漸發展為一個成熟的數學領域。20世紀下半葉,隨著計算機科學的發展,圖論在計算機科學中的應用越來越廣泛,成為計算機科學的一個重要分支。
圖論問題
- 圖的計數:計算某類圖的數量。例如,計算具有個頂點的無向圖的數量。
- 子圖相關問題:在給定的圖中尋找具有特定性質的子圖。例如:
- 子圖同構問題:給定兩個圖和,判斷中是否存在一個子圖與同構。這是一個NP完全問題。
- 哈密頓迴路問題:給定一個圖,判斷是否存在一個子圖與具有個頂點的圈同構。
- 染色問題:將圖的頂點或邊染色,使得滿足特定條件。例如:
- 四色問題:證明任何平面圖的頂點可以用不超過四種顏色染色,使得相鄰頂點具有不同顏色。
- 邊色數問題:求一個圖的最少邊色數,使得相鄰邊具有不同顏色。
- 路徑問題:在給定的圖中尋找滿足特定條件的路徑。例如:
- 柯尼斯堡七橋問題:求解是否存在一條經過柯尼斯堡七橋且僅經過一次的路徑。
- 哈密頓迴路問題:在給定圖中尋找一條包含所有頂點且僅訪問一次的迴路。
- 最小生成樹問題:在給定的帶權無向圖中尋找權值最小的生成樹。
- 中國郵路問題:求解經過所有邊至少一次的最短路徑。
- 最短路問題:求解給定兩個頂點之間的最短路徑。
- 斯坦納樹:求解包含給定頂點集合的最小生成樹。
- 旅行商問題:求解經過所有頂點且僅訪問一次的最短路徑(NP困難問題)。
- 網絡流與匹配問題:
- 最大流問題、最小割問題和最大流最小割定理:在給定的網絡中求解最大流和最小割。
- 最小費用最大流問題:在給定的網絡中求解具有最小費用的最大流。
- 二分圖及任意圖上的最大匹配:求解給定圖中的最大匹配。
- 帶權二分圖的最大權匹配:求解給定帶權二分圖中的最大權匹配。
- 覆蓋問題:
- 最大團:在給定圖中尋找最大的完全子圖。
- 最大獨立集:在給定圖中尋找最大的無邊導出子圖,即獨立集。
- 最小覆蓋集:求解包含所有頂點的最小邊集。
- 最小支配集:求解能支配給定圖中所有頂點的最小頂點集。
重要算法
- 迪克斯特拉算法(Dijkstra's Algorithm, D.A):求解給定圖中兩個頂點之間的最短路徑。
- 克魯斯卡爾算法(Kruskal's Algorithm, K.A):求解給定帶權無向圖的最小生成樹。
- 普里姆算法(Prim's Algorithm, P.A):求解給定帶權無向圖的最小生成樹。
- 拓撲排序算法(Topological Sorting Algorithm, TSA):對有向無環圖(DAG)進行拓撲排序。
- 關鍵路徑算法(Critical Path Algorithm, CPA):求解給定圖中的關鍵路徑。
- 廣度優先搜索算法(Breadth-First Search, BFS):對圖進行廣度優先遍歷。
- 深度優先搜索算法(Depth-First Search, DFS):對圖進行深度優先遍歷。