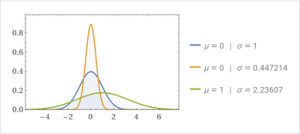
高斯模型,也被稱為正態分布或者高斯分布,是一種在自然和社會科學中廣泛存在的連續概率分布。
定義
高斯模型的概率密度函數(PDF)為: 其中,是均值,是方差。
統計性質
- 均值(Mean):
- 眾數(Mode):
- 標準差(Standard Deviation):
- 方差(Variance):
- 偏度(Skewness):0
累積分布函數
高斯模型的累積分布函數(CDF)為:
百分位數
- 10th:
- 25th:
- 50th:
- 75th:
- 90th:
應用
高斯模型在許多領域都有廣泛的應用。以下是一些具體的應用案例:
1. 信號處理:在信號處理中,噪聲通常被假設為高斯分布。這是因為許多獨立的小效應的總和通常會形成高斯噪聲。
2. 機器學習:在機器學習中,許多算法(如線性回歸、支持向量機等)的誤差項通常被假設為高斯分布。此外,高斯混合模型和高斯過程也是機器學習中常用的模型。
3. 統計質量控制:在製造業中,產品的質量通常被假設為高斯分布。這使得我們可以使用各種統計方法(如控制圖)來監控和改進位造過程。
4. 自然科學:在物理學、生物學等自然科學中,許多現象的測量結果都服從高斯分布。例如,測量誤差、生物種群的身高和體重等。
5. 社會科學:在經濟學、心理學等社會科學中,許多現象也服從高斯分布。例如,人們的收入、智商分數等。
6. 醫學研究:在醫學研究中,許多生物標誌物的測量結果通常服從高斯分布。這使得我們可以使用各種統計方法來分析數據和做出推斷。
7. 金融:在金融中,資產的收益率和價格變動通常被假設為高斯分布。這使得我們可以使用各種統計方法來分析風險和做出投資決策。
8. 天文學:在天文學中,許多測量結果(如星星的亮度、行星的位置等)也服從高斯分布。這使得我們可以使用各種統計方法來分析數據和研究宇宙。
中心極限定理
中心極限定理是高斯分布的一個重要性質,它表明,如果我們從任何一個分布中抽取大量的樣本,那麼這些樣本的平均值將服從高斯分布。這也是為什麼高斯分布在自然和社會科學中如此普遍的原因。
參數估計
對於高斯模型,我們通常使用最大似然估計來估計其參數(均值和方差)。這些參數的最大似然估計可以通過簡單的公式直接計算。
多元高斯分布
除了一元高斯分布,還存在多元高斯分布,用於描述多個隨機變量的聯合分布。多元高斯分布的參數包括一個均值向量和一個協方差矩陣。
高斯過程
高斯過程是一種隨機過程,其任何有限個維度的邊緣分布都是高斯分布。高斯過程在機器學習中有廣泛的應用,例如在高斯過程回歸和高斯過程分類中。
正態性檢驗
在實際應用中,我們通常需要檢驗一個數據集是否服從高斯分布。這可以通過多種正態性檢驗方法來實現,例如Kolmogorov-Smirnov檢驗、Shapiro-Wilk檢驗等。